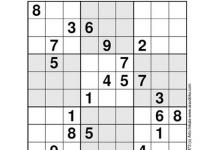
Показывающая связь знака производной с характером монотонности функции.

Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции или ее производной

Если дан график производной , то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины» не интересуют нас в принципе!

Задача 1.

На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.

Решение:

На рисунке выделены цветом области убывания функции :

В эти области убывания функции попадает 4 целые значения .

Задача 2.

На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Решение:

Раз касательная к графику функции параллельна (или совпадает) прямой (или, что тоже самое, ), имеющей угловой коэффициент , равный нулю, то и касательная имеет угловой коэффициент .

Это в свою очередь означает, что касательная параллельна оси , так как угловой коэффициент есть тангенс угла наклона касательной к оси .

Поэтому мы находим на графике точки экстремума (точки максимума и минимума), – именно в них касательные к графику функции будут параллельны оси .

Таких точек – 4.

Задача 3.

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Решение:

Раз касательная к графику функции параллельна (или совпадает) прямой , имеющей угловой коэффициент , то и касательная имеет угловой коэффициент .

Это в свою очередь означает, что в точках касания.

Поэтому смотрим, сколько точек на графике имеют ординату , равную .

Как видим, таких точек – четыре.

Задача 4.

На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых производная функции равна 0.

Решение:

Производная равна нулю в точках экстремума. У нас их 4:

Задача 5.

На рисунке изображён график функции и одиннадцать точек на оси абсцисс:. В скольких из этих точек производная функции отрицательна?

Решение:

На промежутках убывания функции её производная принимает отрицательные значения. А убывает функция в точках. Таких точек 4.

Задача 6.

На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции .

Решение:

Точки экстремума – это точки максимума (-3, -1, 1) и точки минимума (-2, 0, 3).

Сумма точек экстремума: -3-1+1-2+0+3=-2.

Задача 7.

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение:

На рисунке выделены промежутки, на которых производная функции неотрицательная.

На малом промежутке возрастания целых точек нет, на промежутке возрастания четыре целых значения : , , и .

Их сумма:

Задача 8.

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.

Решение:

На рисунке выделены цветом все промежутки, на которых производная положительна, а значит сама функция возрастает на этих промежутках.

Длина наибольшего из них – 6.

Задача 9.

На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наибольшее значение.

Решение:

Смотрим как ведет себя график на отрезке , а именно нас интересует только знак производной .

Знак производной на – минус, так как график на этом отрезке ниже оси .

Задание B8 (ЕГЭ 2013)

На рисунке изображен график функции y=f(x), определенной на интервале от (-5;9). Найдите количество точек, в которых производная функции f(x) равна 0.

Решение

Первое, на что мы обращаем внимание - на рисунке дан график функции (а не производной функции). Далее, отмечаем, что производная функции f(x) равна 0 в точках максимума и минимума функции f(x), т.е. нам нужно найти количество экстремумов функции f(x) на заданном интервале. На языке графика это означает, что нам нужно посчитать количество "бугорков" функции, т.е.:

Получаем, что всего таких точек 9.

Задание B8 (ЕГЭ 2013)

На рисунке изображен график y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .

Решение

Значение производной функции f(x) в точке касания равно угловому коэффициенту касательной. Поэтому нам надо составить уравнение данной касательной и графику и найти угловой коэффициент. В общем случае, уравнение касательной имеет вид: y = kx+b. В этом уравнении k и есть тот самый угловой коэффициент, который мы будет искать.

На рисунке жирными точками отмечены точки, через которые проходит наша касательная. Координаты этих точек: (-4; -2) и (-2; 5). Так как данная прямая проходит через эти точки, то подставим их координаты в уравнение касательной и найдем значение коэффициента k.

2 = -4k+b (подставили точку с координатами (-4;-2));

5 = -2k+b (подставили точку с координатами (-2;5)).

Теперь вычитаем из первого уравнения второе:

2 - 5 = -4k-(-2k);

Получаем искомое значение k=3,5, что то же самое, что значение производной функции f(x) в точке .

Ответ: 3,5.

Задание B8 (ЕГЭ 2013)

На рисунке изображен график y = f"(x) производной функции f(x), определенной на интервале (-2;9). В какой точке отрезка функция f(x) принимает наименьшее значение?

При этом бесконечно малая есть бесконечно малая низшего порядка, чем бесконечно малая.

Определение 3. Если отношение двух бесконечно малых / стремится к единице, т.е. lim / 1 , то бесконечно малые и называются эквива-

лентными бесконечно малыми и пишут.

Пример 2.24. Пусть =х, = ln(1+ х ), где х 0. Бесконечно малые и эквивалентны, так как

			ln(1 x )			ln(1 x ) lim ln[(1 x )1/ x ].
				x 0 x

Приведем без вывода несколько эквивалентных бесконечно малых, использование которых сильно упрощает вычисление пределов:

х sin x, x tg x, x arcsin x , x arctg x , x e x 1 .

3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

3.1. Определение производной и ее геометрический смысл

Предел отношения приращения функции y к, вызвавшему это приращение, приращению аргумента x , при x 0 , т.е.

			f (x0	x) f (x0 )

называется производной функции f (x ) по независимой переменной x .

	Обозначается					Операцию нахождения производной назы-
				dx .
		f (x),

вают дифференцированием.

Угловой коэффициент касательной, проведенной к кривой у =f (x ) в некоторой точке, равен значению производной функции в этой точке. В этом состоит геометрический смысл производной.

Теорема 2. Постоянный множитель можно выносить за знак производ-

ной, т.е. если y cf (x ) , где с = const , то
				cf (x) .
Теорема 3. Производная суммы конечного числа дифференцируемых
функций равна сумме производных этих функций,						т.е. если y u (x ) v (x ) ,
		u (x) v (x) .
Теорема 4. Производная					произведения	двух дифференцируемых

функций равна произведению производной первой функции на вторую плюс произведение производной второй функции на первую, т.е. если y u v , то

y u v v u .

Теорема 5 . Производная частного двух дифференцируемых функций равна дроби, у которой знаменатель равен квадрату знаменателя, а числитель есть разность произведений производной числителя на знаменатель и произ-

	водной знаменателя на числитель, т.е. если

3.3. Производная сложной функции

Пусть дана сложная функция у=f (x ), т.е. такая, что ее можно представить в следующем виде: y=F (u ), u =φ (x ) или y=F (φ (x )). В выражении y=F (u ) переменную u называют промежуточным аргументом.

	Теорема. Если u=φ (x ) имеет в некоторой точке x производную u x (x ) ,
	функция F (u ) имеет при	соответствующем			значении u	производную
y u F (u ) , то сложная функция y=F (φ (x )) в указанной точке x также имеет
производную, которая равна					где вместо u	должно быть
		y x Fu		(u ) x (x ) ,

подставлено выражение u=φ(x).

3.4. Таблица основных формул дифференцирования

Объединим в одну таблицу все основные формулы и правила дифференцирования.

	y const ,				y " 0 .
	y xn ,				y" nxn 1 .
	y x ,				y " 1 .
	y sin x ,				y " cos x .

Непрерывность и дифференцируемость функции.

Теорема Дарбу. Интервалы монотонности.

Критические точки. Экстремум (минимум, максимум).

План исследования функции.

Связь между непрерывностью и дифференцируемостью функции. Если функция f (x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.

С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Достаточные признаки монотонности функции.

Если f ’(x ) > 0 в каждой точке интервала (a, b ), то функция f (x ) возрастает на этом интервале.

Если f ’(x ) < 0 в каждой точке интервала (a, b ) , то функция f (x ) убывает на этом интервале.

Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

Следовательно, функция возрастает на интервалах ( - , 0) и ( 1, + ) и убывает на интервале ( 0, 1 ). Точка x = 0 не входитвобластьопределенияфункции,нопомереприближения x к0 слагаемое x - 2 неограниченновозрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем пост роить график функции ( рис.4б ) .

Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум , рис.5а ,б ).

В точках x 1 , x 2 (рис.5 a ) и x 3 (рис.5 b ) производная равна 0; в точках x 1 , x 2 (рис.5б ) производная не существует. Но все они точки экстремума.

Необходимое условие экстремума. Если x 0 - точка экстремума функции f (x ) и производная f’ существует в этой точке, то f’ (x 0)= 0.

Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f (x ) = x 3 равна 0 при x = 0, но эта функция не имеет экстремум в этой точке (рис.6).

С другой стороны, функция y = | x | , представленная на рис.3, имеет минимум в точке x = 0 , но в этой точке производной не существует.

Достаточные условия экстремума.

Если производная при переходе через точку x 0 меняет свой знак с плюса на минус, то x 0 - точка максимума.

Если производная при переходе через точку x 0 меняет свой знак с минуса на плюс, то x 0 - точка минимума.

План исследования функции. Для построения графика функции нужно:

1) найти область определения и область значений функции,

2) установить, является ли функция чётной или нечётной,

3) определить, является ли функция периодической или нет,

4) найти нули функции и её значения при x = 0,

5) найти интервалы знакопостоянства,

6) найти интервалы монотонности,

7) найти точки экстремума и значения функции в этих точках,

8) проанализировать поведение функции вблизи “особых” точек

И при больших значениях модуля x .

П р и м е р. Исследуйте функцию f (x ) = x 3 + 2 x 2 - x - 2 и постройте график.

Р е ш е н и е. Исследуем функцию по вышеприведенной схеме.

1) областьопределения x R (x – любоедействительное число);

Область значений y R , так как f (x ) – многочлен нечётной

степени;

2) функция f (x ) не является ни чётной, ни нечётной

(поясните, пожалуйста);

3) f (x ) – непериодическая функция (докажите это сами);

4) график функции пересекается с осью Y в точке (0, – 2),

Так как f (0) = - 2 ; чтобы найти нули функции нужно

Решить уравнение: x 3 + 2 x 2 - x - 2 = 0, один из корней

Которого (x = 1) очевиден. Другие корни находятся

(если они есть! ) из решения квадратного уравнения:

x 2 + 3 x + 2 = 0, которое получено делением многочлена

x 3 + 2 x 2 - x - 2 на двучлен ( x – 1). Легко проверить,

Что два других корня: x 2 = - 2 и x 3 = - 1. Таким образом,

Нулями функции являются: - 2, - 1 и 1.

5) Это значит, что числовая ось делится этими корнями на

Четыре интервала знакопостоянства, внутри которых

Функция сохраняет свой знак:

Этот результат может быть получен разложением

многочлена на множители:

x 3 + 2 x 2 - x - 2 = (x + 2) (x + 1 (x – 1)

И оценкой знака произведения .

6) Производная f’ (x ) = 3 x 2 + 4 x - 1 не имеет точек, в которых

Она не существует, поэтому её область определения R (все

Действительные числа); нули f’ (x ) – это корни уравнения:

3 x 2 + 4 x - 1 = 0 .

Полученные результаты сведены в таблицу:

На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Задание На рисунке изображен график производной функции, определенной на интервале. Решение На заданном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Решение Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума.

Вычисление значения производной. Метод двух точек

1. По графику производной исследовать функцию. Функция y=f(x) убывает на промежутках (x1;x2) и (x3;x4). С помощью графика производной y=f ‘(x)также можно сравнивать значения функции y=f(x).

Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты - это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.

В физическом смысле производная — это скорость изменения любого процесса. Материальная точка движется прямолинейно по закону x(t) = t²-13t+23, где x - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения.

Касательная к окружности, эллипсу, гиперболе, параболе.

Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. Учтите, что задан график производной. Как обычно: выколотая точка не лежит на графике, значения в ней не существуют и не рассматриваются. Хорошо подготовленные дети различают понятия «производная» и «вторая производная». Вы путаете: если бы производная обращалась в 0, то в точке функция могла бы иметь минимум или максимум. Отрицательным значениям производной соответствуют интервалы, на которых функция f(x) убывает.

До этого момента мы занимались нахождением уравнений касательных к графикам однозначных функций вида y = f(x) в различных точках.

На рисунке ниже приведены три фактически разных секущих (точки А и В различны), но они совпадают и задаются одним уравнением. Но все же, если отталкиваться от определения, то прямая и ее секущая прямая совпадают. Приступим к нахождению координат точек касания. Просим обратить на него внимание, так как позже мы его используем при вычислении ординат точек касания. Гипербола с центром в точке и вершинами и задается равенством (рисунок ниже слева), а с вершинами и — равенством (рисунок ниже справа). Возникает логичный вопрос, как определить какой из функций принадлежит точка. Для ответа на него подставляем координаты в каждое уравнение и смотрим, какое из равенств обращается в тождество.

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности. Найдем. Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно. А как найти производную, если функция задана не графиком, а формулой?